Physics 1: Work and Energy
The 100 kg box shown below is being pulled along the x-axis by a student. The box slides across a rough surface, and its position varies with time according to the equation , where is in meters and is in seconds.
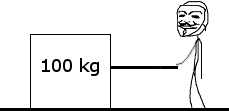
C. Calculate the net work done on the box in the interval = 0 to = 2 s would be greater than, less than, or equal to the answer in part (C). Justify your answer.
The figure below depicts a roller coaster. Assume the roller coaster starts at a velocity of 0 m/s from 70 m.
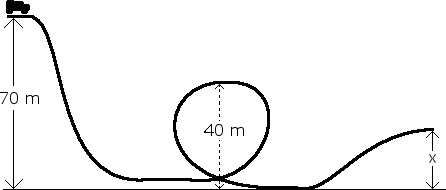
B. Determine the height of the track at point x. It is known that the roller coaster has a velocity of 30 m/s at x.
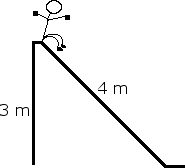
A 20 kg student is about to go down a slide. There is a 3 N frictional force opposing his movement. Assume his velocity at the top of the slide is 0 m/s. Find his velocity at the bottom of the slide.
A student is about to be launched from a spring loaded canon. The student weighs 60 kg and the spring constant is 200 N/kg. Find the students velocity the moment he leaves the canon if the spring is compressed, x = 3 m. Also find the students velocity after the spring has decompressed to x = 2 m.
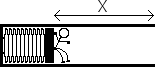
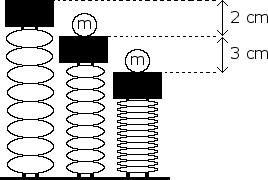
A marble, m, of mass 100 g is placed onto a platform attached to a spring. The weight of the marble compresses the spring 2 cm, as shown below. A force is then applied to the platform to compress the spring an additional 3 cm. When the force is taken away, the spring decompresses and launches the marble upward. What is the maximum height the marble obtains above the unstretched spring (the spring with no mass on it).
A nonlinear spring is compressed various distances x, and the force Frequired to compress it is measured for each distance. The data are shown in the table below.

In an experiment to determine the spring constant of an elastic cord of length 0.60 m, a student hangs the cord from a rod and then attaches a variety of weights to the cord. For each weight, the student allows the weight to hang in equilibrium and then measures the entire length of the cord. The data are recorded in the table below:
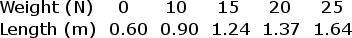
iii. Calculate the maximum speed of the object.
A rubber ball of mass is dropped from a cliff. As the ball falls, it is subject to air drag (a resistive force caused by the air). The drag force on the ball has a magnitude , where is a constant drag coefficient and is the instantaneous speed of the ball. The drag coefficient is directly proportional to the cross-sectional area of the ball and the density of the air and does not depend on the mass of the ball. As the ball falls, its speed approaches a constant value called the terminal speed.
A. Draw and label all the forces on the ball at some instant before it reaches terminal speed.
B. State whether the magnitude of the acceleration of the ball of mass increases, decreases, or remains the same as the ball approaches terminal speed. Explain.
C. Write, but do NOT solve, a differential equation for the instantaneous speed of the ball in terms of time , the given quantities, and fundamental constants.
D. Determine the terminal speed in terms of the given quantities and fundamental constants.
E. Determine the energy dissipated by the drag force during the fall if the ball is released at height and reaches its terminal speed before hitting the ground, in terms of the given quantities and fundamental constants.
A small sphere is moving at a constant speed in a vertical circle. Which of the following quantities is changing?
i. kinetic energy ii. potential energy iii. momentum
i and ii only
i and iii only
i and ii only
ii only
iii only
ii and iii only
In the system of two blocks and a spring shown below, blocks 1 and 2 are connected by a string that passes over a pulley. The initially unstretched spring connects block 1 to a ridged wall. Block 1 is released from rest, initially slides to the right, and is eventually brought to rest by the spring and the friction on the horizontal surface. Which of the following is true of the energy of the system during the process?
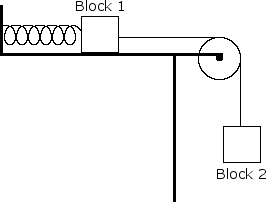
E. The potential energy lost by block 2 is greater in magnitude than the potential energy gained by the spring
In the situation above, after block 1 comes to rest, the force exerted on the rope must be equal in magnitude to
A. Zero
B. the frictional force on block 1
C. the vector sum of the force on block 1 due to the friction and tension in the spring
D. the sum of the weights of the two blocks
E. Shiang doesn't care, he just wants to sleep
F. the difference in the weights of the two blocks
A rope of length is attached to a support at point C. A person of mass sits on a ledge at position A holding the other end of the rope so that it is horizontal and taut, as shown below. The person then drops off the ledge and swings down on the rope toward position B on a lower ledge where an object of mass is at rest. At position B the person grabs hold of the object and simultaneously lets go of the rope. The person and object then land together in the lake at point D, which is a vertical distance below position B. Air resistance and the mass of the rope are negligible. Derive expression for each of the following in terms of , , , and .
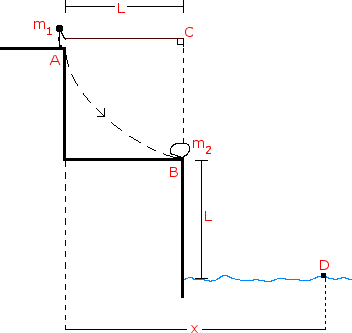
E. The total horizontal displacement x of the person from position A until the person and object land in the water at point D.
A spherical non rotating planet has a radius R and a uniform density throughout its volume. Suppose a narrow tunnel were drilled through the planet along one of its diameters as shown in the figure below, in which a small ball of mass m could move freely under the influence of gravity. Let r be the distance of the ball from the center of the planet. Suppose the ball is dropped into the tunnel from rest at the planet's surface.
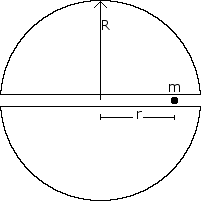
F. Write an equation that could be used to calculate the time it takes the ball to move from point P to the center of the planet.
A solid brass block of mass m slides along a frictionless track when released from rest along the straight section. The circular loop has a radius R.
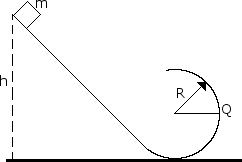
B. Assume the block is released at height h = 6.0 R, what are the magnitude and direction of the horizontal force competent acting on the block at point Q?
A 50 kg object is to be launched 7 x 10 m out into space (not into orbit, it will fall back to earth). Given that the radius of the earth is 6.4 x 10 m and the mass of the earth is 6.0 x 10 kg, find:
A. The work done to put the object that far into space.
B. The total kinetic energy of the object required to put the object that far into space.
C. The binding energy.
D. The escape velocity.
A 60 kg object is to be launched into orbit, 7 x 10 m above the Earth's surface. Given that the radius of the earth is 6.4 x 10 m and the mass of the earth is 6.0 x 10 kg, find:
A. The work done to put the object into orbit.
B. The velocity required to put the object into orbit.
C. The velocity of the object once it is in orbit.