Frictional Force Problem

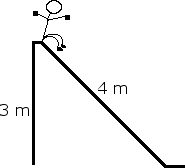
A 20 kg student is about to go down a slide. There is a 3 N frictional force opposing his movement. Assume his velocity at the top of the slide is 0 m/s. Find his velocity at the bottom of the slide.

A student is about to be launched from a spring loaded canon. The student weighs 60 kg and the spring constant is 200 N/kg. Find the students velocity the moment he leaves the canon if the spring is compressed, x = 3 m. Also find the students velocity after the spring has decompressed to x = 2 m.

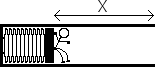
A rope of length $L$ is attached to a support at point C. A person of mass $m_1$ sits on a ledge at position A holding the other end of the rope so that it is horizontal and taut, as shown below. The person then drops off the ledge and swings down on the rope toward position B on a lower ledge where an object of mass $m_2$ is at rest. At position B the person grabs hold of the object and simultaneously lets go of the rope. The person and object then land together in the lake at point D, which is a vertical distance $L$ below position B. Air resistance and the mass of the rope are negligible. Derive expression for each of the following in terms of $m_1$ , $m_2$ , $L$ , and $g$.

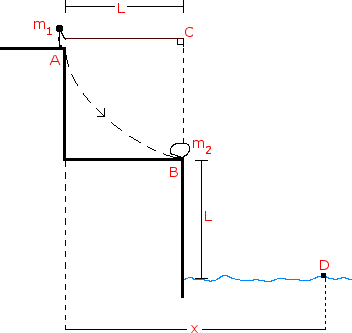
E. The total horizontal displacement x of the person from position A until the person and object land in the water at point D.

A spherical non rotating planet has a radius R and a uniform density $ho$ throughout its volume. Suppose a narrow tunnel were drilled through the planet along one of its diameters as shown in the figure below, in which a small ball of mass m could move freely under the influence of gravity. Let r be the distance of the ball from the center of the planet. Suppose the ball is dropped into the tunnel from rest at the planet's surface.

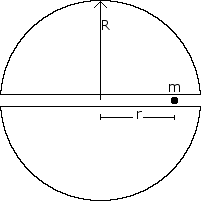
F. Write an equation that could be used to calculate the time it takes the ball to move from point P to the center of the planet.