Gravity Physics
A spherical non rotating planet has a radius R and a uniform density throughout its volume. Suppose a narrow tunnel were drilled through the planet along one of its diameters as shown in the figure below, in which a small ball of mass m could move freely under the influence of gravity. Let r be the distance of the ball from the center of the planet. Suppose the ball is dropped into the tunnel from rest at the planet's surface.
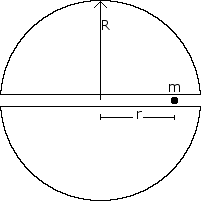
F. Write an equation that could be used to calculate the time it takes the ball to move from point P to the center of the planet.
SOLUTION MISSING: Unfortunately the author of this youtube video removed their content. You may be able to find a similar problem by checking the other problems in this subject. If you want to contribute, leave a comment with the link to your solution.Related Problems
The figure below depicts a roller coaster. Assume the roller coaster starts at a velocity of 0 m/s from 70 m.
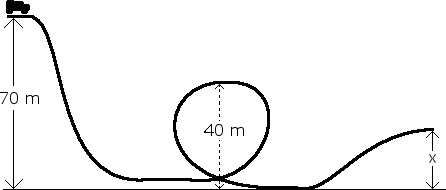
B. Determine the height of the track at point x. It is known that the roller coaster has a velocity of 30 m/s at x.
A 20 kg student is about to go down a slide. There is a 3 N frictional force opposing his movement. Assume his velocity at the top of the slide is 0 m/s. Find his velocity at the bottom of the slide.
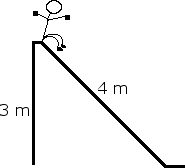
A student is about to be launched from a spring loaded canon. The student weighs 60 kg and the spring constant is 200 N/kg. Find the students velocity the moment he leaves the canon if the spring is compressed, x = 3 m. Also find the students velocity after the spring has decompressed to x = 2 m.
A solid brass block of mass m slides along a frictionless track when released from rest along the straight section. The circular loop has a radius R.
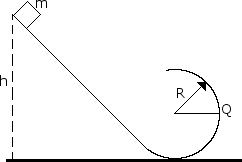
B. Assume the block is released at height h = 6.0 R, what are the magnitude and direction of the horizontal force competent acting on the block at point Q?