Physics 1: Uniform Circular Motion

A car of mass 100 kg is traveling in a circle of radius 20 m. There is a frictional force of 500 N on the car's wheels (in the direction of the center of the circle, to keep the car going in a circle). Draw a free body diagram for the car and find the velocity of the car.

A student is swinging a mass, m = 2.0 kg, in a uniform vertical circle of radius R = 2.5 m. The period of the rotation is 2.8 seconds. Draw a free body diagram for the mass at the top of the circle and find the tension of the string (ignore friction and the mass of the string.) Repeat for the mass at the bottom of the rotation.

A car is driving in a circle on an embanked road as shown below. Draw a free body diagram for the car, ignoring friction.

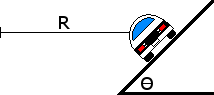
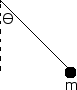
A 1.2 kg mass, m, is swinging on a string pendulum of length 80 cm (the string has negligible mass). As shown in the figure below, when ##\theta## is 10 degrees the velocity of the mass is 0.6 m/s. Find the tension in the string and the acceleration of the mass at this moment.

Given that the radius of orbit for the moon is 3.8 x 10##^8## m, the period of the moon's orbit is 2.36 x 10##^6## s, and the radius of the earth is 6.38 x 10##^6## m; Find the altitude of a geostationary satellite.(hint: use Kepler's third law.)

Find the period of a satellite at an altitude of 200 km.
R##_E## = 6.38 x 10##^6## m
M##_E## = 5.98 x 10##^{24}## kg
G = 6.67 x 10##^{-11}## ##\frac{Nm^2}{kg^2}##