Physics 1: Rotational Dynamics

Expand

All Physics 1 Vectors Kinematics Free Body Diagrams Uniform Circular Motion Work and Energy Impulse and Momentum Rotational Dynamics Simple Harmonic Motion

Rotational Kinematics

The wheel shown below has eight equally spaced spokes and a radius of 30 cm. It is mounted on a fixed axle and is spinning at 2.5 rev/sec. You want to shoot a 20 cm long arrow without hitting any of the spokes. Assume the arrow and the spokes are very thin.
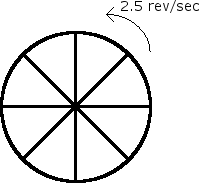
rotational kinematics problem solution > A. What minimum speed must the arrow have?<br

B. Does it matter where between the axle and the rim of the wheel you aim? If so what is the best location?

Rotational Physics

A flywheel turns through 40 rev as it slows from an angular speed of 1.5 rad/s to stop.
A. Assuming constant angular acceleration find the time for it to come to rest.
B. What is its angular acceleration?
C. How much time is required for it to complete its first 20 of the 40 revolutions?

Rotational Inertia

A massless string is wrapped around a disk of rotational inertia I = ##\frac{1}{2} m R^2## . The disk falls and spins as it falls, unraveling the rope. Determine the tension in the string and the acceleration of the disk.
yoyo rotational inertia torque

Mass Moment Inertia

A solid brass sphere of mass m and radius r << R rolls along a track when released from rest along the straight section. The circular loop has a radius R.
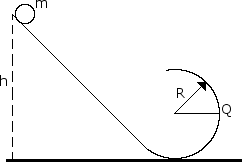
brain puzzles IQ tests > A. What is h in terms of R if the sphere is on the verge of leaving the track when it reaches the top of the loop? <br

brain puzzles IQ tests ><br />A. What is h in terms of R if the sphere is on the verge of leaving the track when it reaches the top of the loop? <br

B. Assume the sphere is released at height h = 6.0 R, what are the magnitude and direction of the horizontal force competent acting on the sphere at point Q?

Rotational Kinetic Energy

A pulley of radius ##R_1## and rotational inertia ##I_1## is mounted on an axle with negligible friction. A light cord passing over the pulley has two blocks of mass ##m## attached to either end, as shown below. Assume that the cord does not slip on the pulley. Determine the answers to parts (A) and (B) in terms of ##m## , ##R_1## , ##I_1## , and fundamental constants.
$rotational inertia physics question > A. Determine the tension T in the cord B. One block is now removed from the right and hung on the left. When the system is released from rest, the three blocks on the left accelerate downward with an acceleration ##\frac{g}{3}## . Determine the following<ul><li>The tension ##T_3## in the section of cord supporting the three blocks on the left</li><li>The tension ##T_1## in the section of cord supporting the single block on the right</li><li>The rotational inertia ##I_1## of the pulley</li></ul> C. The blocks are now removed and the cord is tied into a loop, which is passed around the original pulley and a second pulley of radius ##2R_1## and rotational inertia ##16I_1## . The axis of the original pulley is attached to a motor that rotates it at angular speed ##\omega_1## , which in turn causes the larger pulley to rotate. The loop does not slip on the pulleys. Determine the following in terms of ##I_1## , ##R_1## , and ##\omega_1## . <img$

Orbital Velocity

An explorer plans a mission to place a satellite into a circular orbit around the planet Jupiter, which has a mass of ##M_1## = 1.90 x 10##^{27}## kg and radius ##R_1## = 7.14 x 10##^7## m.
A. If the radius of the planned orbit is ##R## , use Newton's laws to show each of the following.

The orbital speed of the planned satellite is give by ##v## = ##\sqrt{\frac{GM_1}{R}}## .
The period of the orbit is given by ##T## = ##\sqrt{\frac{4\pi^2R^3}{GM_1}}##

B. The explorer wants the satellite's orbit to be synchronized with Jupiter's rotation. This requires an equatorial orbit whose period equals Jupiter's rotation period of 9 hr 51 min = 3.55 x 10##^5## s. Determine the required orbital radius in meters.
C. Suppose that the injection of the satellite into orbit is less than perfect. For an injection velocity that differs form the desired value in each of the following ways, sketch the resulting orbit on the figure. ( J is the center of Jupiter, the dashed circle is the desired orbit, and ##P## is the injection point.) Also, describe the resulting orbit qualitatively but specifically

When the satellite is at the desired altitude over the equator, its velocity vector has the correct direction, but the speed is slightly faster than the correct speed for a circular orbit of that radius.
When the satellite is at the desired altitude over the equation, its velocity vector has the correct direction but the speed is slightly slower than the correct speed for a circular orbit of that radius.

Rotational Kinetic Energy Physics Problem

A light string that is attached to a large block of mass 4m passes over a pulley with negligible rotational inertia and is wrapped around a vertical pole of radius r, as shown below. The system is released from rest, and as the block descends the string unwinds and the vertical pole with its attached apparatus rotates. The apparatus consists of a horizontal rod of length 2L, with a small block of mass m attached at each end. The rotational inertia of the pole and the rod are negligible.

kinetic energy physics problem ><br />A. Determine the rotational inertia of the rod and block apparatus attached at the top of the pole.<br />B. Determine the downward acceleration of the large block<br />C. When the large block has descended a distance D, how does the instantaneous total kinetic energy of the three blocks compare with the value 4mgD?<ul><li>Greater than 4mgD</li><li>Equal to 4mgD</li><li>Less than 4mgD</li></ul>The system is now reset. The string is rewound around the pole to bring the large block back to its original location. The small blocks are detached form the rod and then suspended from each end of the rod, using strings of length ##l## . The system is again released from rest so that as the large block descends and the apparatus rotates, the small blocks swing outward, as shown below.<br /><img

D. When the large block has descended a distance D, how does the instantaneous total kinetic energy of the three blocks compare to that in part (C), Greater, Equal, or Less?

Moment of Inertia

A uniform disk is mounted to an axle and is free to rotate without friction. A thin uniform rod is rigidly attached to the disk so that it will rotate with the disk. A block is attached to the end of the rod. Properties of the disk, rod, and block are as follows.
$physics moment of inertia problem > Disk: mass = 3m, radius = R, moment of inertia about center ##I_D## = ##\frac{3}{2}mR^2## Rod: mass = m, radius = 2R, moment of inertia about one end ##I_R## = ##\frac{4}{3}mR^2## Block: mass = 2m The system is held in equilibrium with the rod at an angle ##\theta_0## to the vertical as shown above, by a horizontal string of negligible mass with one end attached to the disk at the other to a wall. Express your answers to the following in terms of m, R, ##\theta_0## , and g. A. Determine the tension in the string The string is now cut and the disk rod block system is free to rotate B. Determine the following for the instant immediately after the string is cut<ul><li>The magnitude of the angular acceleration of the disk</li><li>The magnitude of the linear acceleration of the mass at teh end of the rod</li></ul><img$ C. Determine the linear speed of the mass at the end of the rod for the instant the rod is in the horizontal position.

Moment of Inertia Disk

A solid disk of unknown mass and known radius R is used as a pulley in a lab experiment as shown below. A small block of mass m is attached to a string, the other end of which is attached to the pulley and wrapped around it several times. The block of mass m is released from rest and takes a time t to fall the distance D to the floor.
physics rotational inertia problem > A. Calculate the linear acceleration ##a## of the falling block in terms of the given quantities. B. The time t is measured for various heights D and the data are recorded in the following table. <img

physics rotational inertia problem ><br />A. Calculate the linear acceleration ##a## of the falling block in terms of the given quantities.<br />B. The time t is measured for various heights D and the data are recorded in the following table.<br /><img

D. The value of acceleration found in (B)iii, along with numerical values for the given quantities and your answer to (C), can be used to determine the rotational inertia of the pulley. The pulley is removed from its support and its rotational inertia is found to be greater than this value. Give one explanation for this discrepancy.

Oscillation Physics

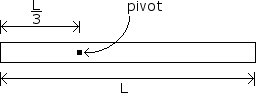
A uniform rod of mass M and length L is attached to a pivot of neglible friction as shown below. The pivot is located at a distance ##\frac{L}{3}## from the left end of the rod. Express all answers in terms of the given quantities and fundamental constants.

physics pivot oscillation problem ><br />A. Calculate the rotational inertia of the rod about the pivot.<br />B. The rod is then released from rest from teh horizontal positon shown above. Calculate the linear speed of the bottom end of the rod when the rod passes through teh vertical.<br />C. The rod is brought to rest in teh vertical posoition shown below and hangs freely. It is then displace slightly from this position. Calculate the period of teh osciallation as it swings.<br /><img

Rotational Dynamics

A system consists of a ball of mass ##M_2## and a uniform rod of mass ##M_1## and length ##d##. The rod is attached to a horizontal frictionless table by a pivot at point ##P## and initially rotates at an angular speed ##\omega##, pictured below on the left. The rotational inertia of the rod about point ##P## is ##\frac{1}{3}M_1d^2## . The rod strikes the ball, which is initially at rest. As a result of this collision, the rod is stopped and the ball moves in the direction shown on the right. Express all answers in terms of ##M_1## , ##M_2## , ##\omega## , ##d## , and fundamental constants.
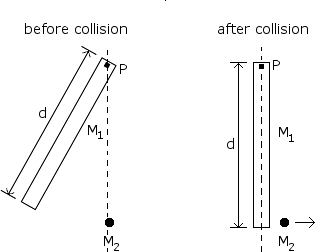
$physics angular momentum problem > A. Derive an expression for the angular momentum of the rod about point ##P## before the collision. B. Derive an expression for the speed ##v## of the ball after the collision. C. Assume that this collision is elastic, calculate the numerical value of the ratio ##\frac{M_1}{M_2}##. <img$ D. A new ball with the same mass ##M_1## as the rod is now placed a distance ##x## from the pivot, as shown above. Again assuming the collision is elastic, for what value ##x## will the rod stop moving after hitting the ball?

Orbital Energy Problem

In March 1999 the Mars Global Surveyor (GS) entered its final orbit about Mars, sending data back to Earth. Assume a circular orbit with a period of 1.18 x 10 ##^2## minutes = 7.08 x 10 ##^3## m/s. The mass of the GS is 930 kg and the radius of Mars is 3.43 x 10##^6## m .
A. Calculate the radius of the GS orbit.
B. Calculate the mass of Mars.
C. Calculate the total mechanical energy of the GS in this orbit.
D. If the GS was to be placed in a lower circular orbit (closer to the surface of Mars), would the new orbital period of the GS be greater than or less than the given period?
E. In fact, the orbit of the GS entered was slightly eliptical with its closest approach to Mars at 3.71 x 10 ##^5## m above the surface and its furthest distance at 4.36 x 10 ##^5## m above the surface. If the speed of the GS at closest approach is 3.40 x 10 ##^3## m/s, calculate the speed at the furthest point of the orbit.