Oscillation Physics
A uniform rod of mass M and length L is attached to a pivot of neglible friction as shown below. The pivot is located at a distance from the left end of the rod. Express all answers in terms of the given quantities and fundamental constants.
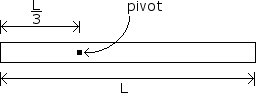 SOLUTION MISSING: Unfortunately the author of this youtube video removed their content. You may be able to find a similar problem by checking the other problems in this subject. If you want to contribute, leave a comment with the link to your solution.
SOLUTION MISSING: Unfortunately the author of this youtube video removed their content. You may be able to find a similar problem by checking the other problems in this subject. If you want to contribute, leave a comment with the link to your solution.Related Problems
A flywheel turns through 40 rev as it slows from an angular speed of 1.5 rad/s to stop.
A. Assuming constant angular acceleration find the time for it to come to rest.
B. What is its angular acceleration?
C. How much time is required for it to complete its first 20 of the 40 revolutions?
A massless string is wrapped around a disk of rotational inertia I = . The disk falls and spins as it falls, unraveling the rope. Determine the tension in the string and the acceleration of the disk.

A solid brass sphere of mass m and radius r << R rolls along a track when released from rest along the straight section. The circular loop has a radius R.
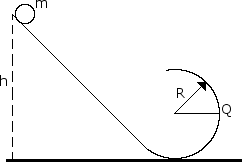
B. Assume the sphere is released at height h = 6.0 R, what are the magnitude and direction of the horizontal force competent acting on the sphere at point Q?
A system consists of a ball of mass and a uniform rod of mass and length . The rod is attached to a horizontal frictionless table by a pivot at point and initially rotates at an angular speed , pictured below on the left. The rotational inertia of the rod about point is . The rod strikes the ball, which is initially at rest. As a result of this collision, the rod is stopped and the ball moves in the direction shown on the right. Express all answers in terms of , , , , and fundamental constants.
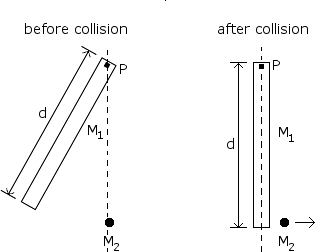
D. A new ball with the same mass as the rod is now placed a distance from the pivot, as shown above. Again assuming the collision is elastic, for what value will the rod stop moving after hitting the ball?