Orbital Energy Problem
In March 1999 the Mars Global Surveyor (GS) entered its final orbit about Mars, sending data back to Earth. Assume a circular orbit with a period of 1.18 x 10 minutes = 7.08 x 10 m/s. The mass of the GS is 930 kg and the radius of Mars is 3.43 x 10 m .
A. Calculate the radius of the GS orbit.
B. Calculate the mass of Mars.
C. Calculate the total mechanical energy of the GS in this orbit.
D. If the GS was to be placed in a lower circular orbit (closer to the surface of Mars), would the new orbital period of the GS be greater than or less than the given period?
E. In fact, the orbit of the GS entered was slightly eliptical with its closest approach to Mars at 3.71 x 10 m above the surface and its furthest distance at 4.36 x 10 m above the surface. If the speed of the GS at closest approach is 3.40 x 10 m/s, calculate the speed at the furthest point of the orbit.
SOLUTION MISSING: Unfortunately the author of this youtube video removed their content. You may be able to find a similar problem by checking the other problems in this subject. If you want to contribute, leave a comment with the link to your solution.Related Problems
The wheel shown below has eight equally spaced spokes and a radius of 30 cm. It is mounted on a fixed axle and is spinning at 2.5 rev/sec. You want to shoot a 20 cm long arrow without hitting any of the spokes. Assume the arrow and the spokes are very thin.
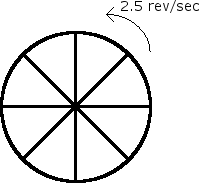
B. Does it matter where between the axle and the rim of the wheel you aim? If so what is the best location?
A flywheel turns through 40 rev as it slows from an angular speed of 1.5 rad/s to stop.
A. Assuming constant angular acceleration find the time for it to come to rest.
B. What is its angular acceleration?
C. How much time is required for it to complete its first 20 of the 40 revolutions?
A massless string is wrapped around a disk of rotational inertia I = . The disk falls and spins as it falls, unraveling the rope. Determine the tension in the string and the acceleration of the disk.

A solid brass sphere of mass m and radius r << R rolls along a track when released from rest along the straight section. The circular loop has a radius R.
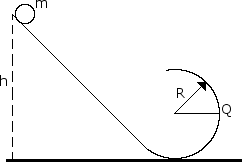
B. Assume the sphere is released at height h = 6.0 R, what are the magnitude and direction of the horizontal force competent acting on the sphere at point Q?