Nonlinear Spring Problem

A 20 kg student is about to go down a slide. There is a 3 N frictional force opposing his movement. Assume his velocity at the top of the slide is 0 m/s. Find his velocity at the bottom of the slide.

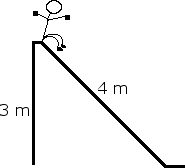
A student is about to be launched from a spring loaded canon. The student weighs 60 kg and the spring constant is 200 N/kg. Find the students velocity the moment he leaves the canon if the spring is compressed, x = 3 m. Also find the students velocity after the spring has decompressed to x = 2 m.

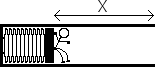
In an experiment to determine the spring constant of an elastic cord of length 0.60 m, a student hangs the cord from a rod and then attaches a variety of weights to the cord. For each weight, the student allows the weight to hang in equilibrium and then measures the entire length of the cord. The data are recorded in the table below:

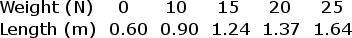
iii. Calculate the maximum speed of the object.

A rubber ball of mass $m$ is dropped from a cliff. As the ball falls, it is subject to air drag (a resistive force caused by the air). The drag force on the ball has a magnitude $bv^2$ , where $b$ is a constant drag coefficient and $v$ is the instantaneous speed of the ball. The drag coefficient $b$ is directly proportional to the cross-sectional area of the ball and the density of the air and does not depend on the mass of the ball. As the ball falls, its speed approaches a constant value called the terminal speed.

A. Draw and label all the forces on the ball at some instant before it reaches terminal speed.

B. State whether the magnitude of the acceleration of the ball of mass $m$ increases, decreases, or remains the same as the ball approaches terminal speed. Explain.

C. Write, but do NOT solve, a differential equation for the instantaneous speed $v$ of the ball in terms of time $t$ , the given quantities, and fundamental constants.

D. Determine the terminal speed $v_t$ in terms of the given quantities and fundamental constants.

E. Determine the energy dissipated by the drag force during the fall if the ball is released at height $h$ and reaches its terminal speed before hitting the ground, in terms of the given quantities and fundamental constants.