Physics 2: Electric Forces and Fields

Point A is a distance d = 0.5 m from the center of a charged rod. The rod has a charge of + 1 nC and is X = 4 m long. Find the electric field at point A.

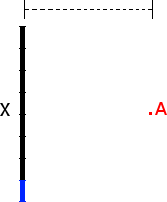
The rod below is 1.4 m long and carries a charge of -8 x 10##^{-8}##. Point A is 0.7 m from the center of the rod. Find the electric field at point A due to the bottom 1/8th of the rod, colored blue below.

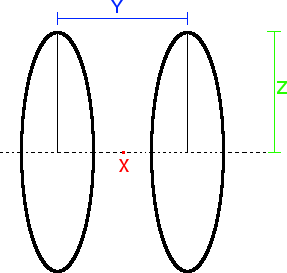
Two concentric loops are shown below, with a distance between them Y = 0.4 m, a radius Z = 0.1 m. The loop on the left has a charge of +9 nC and the loop on the right has a charge of -9 nC. Find the electric field at point X, which is directly in the middle of the loops.

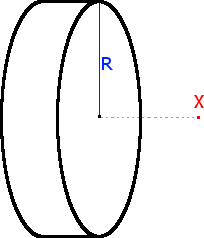
A disk with radius R = 0.4 m carries a +4 ##\mu##C. Find the electric field at point X, a distance of 0.001 m from the center of the disk.

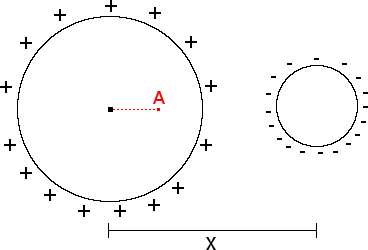
Below are two charged spheres separated by a distance, X = 0.1 m from center to center. The sphere on the left carries a charge of 10 nC and has a radius 0.01 m. The sphere on the right carries a charge of -2 nC. Find the electric field at point A, which is 0.005 m from the center of the large sphere.

Given the 3 dimensional electric field, ##\vec{E}## = 200 ##\frac{N}{C}## ##\hat{i}## + 300 ##\frac{N}{C}## ##\hat{j}## + 400 ##\frac{N}{C}## ##\hat{k}## , and an area vector ##\vec{A}## = 0.2 m##^2## ##\hat{i}## + 0.3 m##^2## ##\hat{j}##, find the electric flux. (this is a calculus based physics problem)

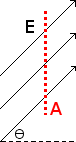
Below is a figure depicting a uniform electric field, E = 400 N/C at an angle ##\theta## = 40##^\circ## above the horizontal. The red line represents a rectangle, going into the page, with area, A = 0.20 m##^2##. Find the electric flux through the rectangle.

A uniformly charged sphere has a radius of 40 cm and a total charge of 80 nC spread throughout its volume. If the following sections were removed from the sphere, how much charge would they contain?
A. A Spherical section with a radius of 10 cm
B. A cubical section with sides of 5.0 cm
C. A cylindrical section with radius 8.0 cm and length 15 cm

A very long cylindrical insulator with a radius of 30 cm has a volumetric charge density of -80 ##\frac{nC}{m^2}##. What is the volume of the electric field a distance of 10 cm away from the center? 30 cm from the center? 50 cm from the center?

Use Gauss's law to find the electric field around a conducting sphere of radius R, both within and outside the sphere. That is for a distance rR. (this is a calculus based derivation)