Calculus 1: Optimization Problems
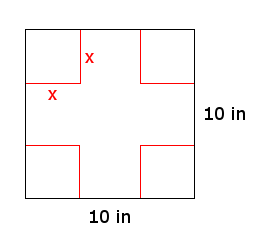
An open box is made by cutting and folding a 10x10 inch square of cardboard as shown below. Find the maximum volume the open box can attain by altering the length of cuts, x.
Maximize the product of two numbers, x and y, given that the first number squared added to the second number is equal to 27.
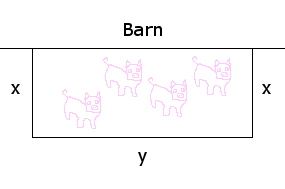
A dudebro has 500 feet of fencing to make a pig pen along a barn as shown below. Find the maximum area.
A rectangle has a perimeter of 40 feet. Find the width and height of a rectangle with a maximum area.
Find two non-negative numbers, x and y, whose sum is 9 with a maximum product of x and the square of y,
Find the maximum value of on
A company makes wrenches. It costs them an initial \$10,000 to set up and an additional \$5.00 for each wrench. A market study indicates that if the price of a wrench is \$5.00 then the company will sell 200,000 wrenches. However, for every \$10 that the company raises the price per wrench, only half as many people will buy the wrench. What price should they charge per wrench to maximize the companies profits.
You have been asked to design a 1 liter can in the shape of a right circular cylinder. What dimensions use the least amount of material for the can? (minimize surface area)
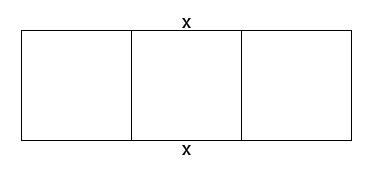
A man has 1000 feet of fencing material and he wants to enclose three adjacent pens for his three dogs as shown below. What dimensions should be used to maximize the total enclosed area? What is the final maximum total area?