Calculus 1: Applications of Integration

Find the area between the two curves $y = x^4 - 2x^2$ and $y = 2x^2$

Find the area bounded by the following curves/lines

$y = x + 1$

$y = 9 - x^2$

$x = -1$

$x = 2$

Find the area between the curves $y = x$ and $y = x^2$

Compute the area between $y = \sin{x}$ and $y = \cos{x}$ and the interval $[\frac{\pi}{4}, \frac{5\pi}{4}]$

Compute the area of the region bounded by the curves $y = x^3$ and $y = 3x - 2$

Find the average value on $[0, 16]$ of $f(x) = \sqrt{x}$

What is the average value of the function $f(x) = 3x^2 - 2x$ on $[1, 4]$

Find the average value of the function $h(x) = \cos^4{(x)}\sin(x)$ on $[0, \pi]$

Determine the volume of the solid generated by rotating the function about the x-axis on $[0,3]$

$y = \sqrt{9 - x^2}$

Determine the volume of the solid generated by rotating the function about the y-axis on $[0,4]$

$y = \sqrt{x}$

Use the shell method to determine the volume formed by the bounded region rotated about the x-axis.

$y = x^2$, $y = 0$, $x = 2$

Use the shell method to determine the volume of the solid formed by rotating the region about the y axis.

$y = x^2 + 2$

$y = 0$, $x = 0$, $x = 2$

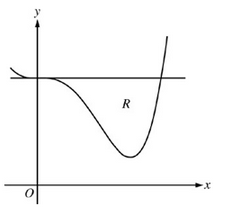
Let R be the region enclosed by the graph of $f(x) = x^4 - 2.3x^3 + 4$ and the horizontal line y = 4, as shown in the figure above.

A. Find the volume of the solid generated when R is rotated about the horizontal line y = -2

B. Region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in R. Find the volume of the solid.

C. The vertical line x = k divides R into two regions with equal areas. Write, but do not solve, an equation involving integral expressions whose solution gives the value k.

Use the disk method to find the volume of the solid of rotation by rotating the bounded area around the y-axis

$y = 2x^2$, $y = 0$, $x = 2$

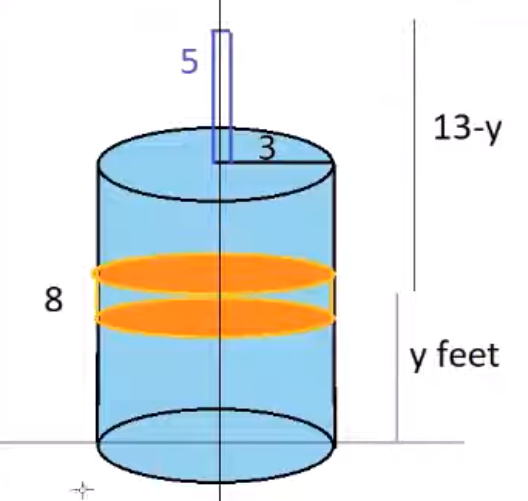
A cylindrical tank is full of water and its radius is 3 feet and height is 8 feet. Find the work done pumping the water out of the tank through a pipe which rises 5 feet above the top of the tank. Assume that water weighs 62.5 lbs/ft^3

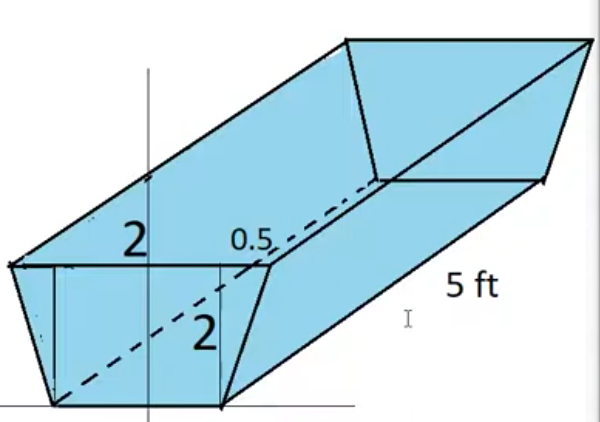
The water trough is 5 feet long and its ends are trapezoids as shown. If the water trough is full of water, find work done in pumping the water out over the top. Assume that water weighs 62.5 lbs/ft^3.