Physics 2

What is the resonant frequency of sound when you blow across an empty soda bottle that is 15 cm tall?

Two point charges, q$_1$ = 6Q and q$_2$ = -2Q, are separated by a distance, d. The attractive force between these two particles is 20 N. If the distanced is halved, so d$_2$ = d/2, what is the new force between the particles?

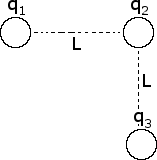
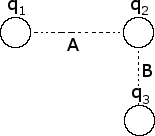
In the figure below, A = 3 cm, B = 1 cm, q$_1$ = +15 nC, q$_2$ = -5 nC, and q$_3$ is -10 nC. Find the magnitude and direction of the net electrostatic force on q$_3$

A proton ( 1.6 x 10$^{-19}$ C ) is placed 2.19 x 10$^{-6}$ m from point A. Find the electric field at point A. Imagine a proton is put at point A. Find the force that acts on the proton.

Two parallel charged plates, one with a surface charge density of $\eta_1$ = 40 $\frac{nC}{m^2}$ and another, $\eta_2$ = -60 $\frac{nC}{m^2}$. Find the total electric field between the plates. (note this is not a capacitor)

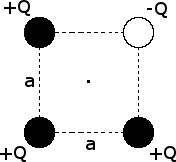
The electron gun in a television tube is used to accelerate electrons from rest to 3.0 x 10$^7$ m/s within a distance of 2.0 cm. What electric field is required? Should the electric field be in the same or opposite direction of the electrons motion?

The figure below shows a single dipole of charges $\pm$5 nC, with a distance s = 0.002 m between the poles. Point A is a distance, d = 0.1 m, and is perpendicular to the dipole. Point B is a vertical distance, d = 0.1 m, and is parallel to the dipole. Find the electric field at points A and B.

Two dipoles are placed a distance, d = 0.05 m, from the point A (labeled in red). The distance between dipoles is s = 0.01 m. Each dipole consists of a positive and negative charge of $\pm$2 nC. Find the electric field at point A.

Two concentric loops are shown below, with a distance between them Y = 0.4 m, a radius Z = 0.1 m. The loop on the left has a charge of +9 nC and the loop on the right has a charge of -9 nC. Find the electric field at point X, which is directly in the middle of the loops.

Given the 3 dimensional electric field, $\vec{E}$ = 200 $\frac{N}{C}$ $\hat{i}$ + 300 $\frac{N}{C}$ $\hat{j}$ + 400 $\frac{N}{C}$ $\hat{k}$ , and an area vector $\vec{A}$ = 0.2 m$^2$ $\hat{i}$ + 0.3 m$^2$ $\hat{j}$, find the electric flux. (this is a calculus based physics problem)

A sphere carries a charge of +2 nC. Point A is X = 0.02 m to the direct right of the sphere, and point B is Y = 0.06 m to the right of the sphere. Find the electrostatic potential difference from A to B. (the solution involves calculus)

A very long thin wire carries a line charge density, $\lambda$ = 361.0 $\frac{nC}{m}$. Find the electric potential difference between points 3.0 m and 6.0 m on a perpendicular radius to the axis of the wire, provided the perpendicular radius is not near either end of the wire. (this problem requires calculus)

A circuit has 2 capacitors in parallel, A = 20 $\mu$F, B = 10 $\mu$F, with a 10 V battery. Find the potential difference across each capacitor, and the charge of each capacitor.

What are the voltage drops across each capacitor? How much energy will capacitor C store?

The battery is 12 V

A circuit has the following R = 20 $\Omega$, C = 25 $\mu$F, $\Delta{V}_C$ = 10 V.

How long will it take for the charge to drop to one third its original value?

Determine the direction of the magnetic force acting on the proton or electron in each situation below.

A.

B.

The picture below depicts a wire carrying a current I = 25.0 A. The shape of the wire is two combined arcs with r$_1$ = 9.0 cm and r$_2$ = 6.0 cm. Find the magnetic field at the center of the arcs (in blue).

As a steel guitar string vibrates, the component of the magnetic field perpendicular to the area of a pickup coil nearby is given by B(t) = 50 mT + (3.20 mT) Sin (1046$\cdot\pi$t). The circular pickup coil has 30 turns, a radius of 2.70 mm, and a resistance of 0.10 $\Omega$. What is the magnitude of the maximum current induced in the coil?

A rectangular wire loop rests in a magnetic field as shown. Points Y and Z are grasped and pulled tight so that the area of the loop becomes zero. Determine the direction of the current through the resistor.

A conductive ring is falling through a magnetic field as shown below.

A. Sketch the direction of the induced current at each location

B. Where is the induced current the greatest?