You are looking into a shiny Christmas ornament (ball). The ball has a diameter of 8.0 cm. Where does your image appear to be if you are holding the ball 20 cm from your face? What is the magnification?
A convex mirror in a store has a radius of curvature of 0.55 m. If a customer is 10 m from the mirror, where is the customer's image in the mirror? What is the magnification of the image of the image? What is the orientation of the image?
A concave mirror has a focal length of 40 cm. Determine the object position for which the resulting image is upright and 4 times the size of the object.
You want to form an image on a screen 10 m from a mirror. If the image is 7 times bigger than the object, what type of mirror do you need? What is the radius of curvature?
An object is placed at a distance of 30 cm from a concave lens of focal length 15 cm, hI = 2 cm. Determine the position of the image, the linear magnification, and h0.
The image of a tree on a 35 mm color slide is 1.8 mm high. It is to be projected onto a screen 3.0 m from the slide and is to appear 493 mm high. What focal length is needed?
Given an object height of 3 cm and a convex lens of focal length 10cm. Determine the position and size of the produced image if the object is placed at:
A. 30 cm
B. 5 cm
A light bulb is placed to the left of a convex lens of focal length 20 cm. The image formed is enlarged 5 times and is to the right of the lens. Find the image distance and the object distance.
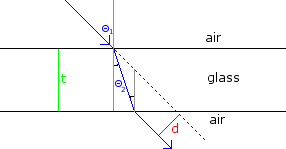
A plate of glass, with thickness t (green), is shown below. Find the distance, d (in red), that the ray is displaced.
A telescope is constructed with two lenses separated by 25 cm. The focal length of the objective is 20 cm. The focal length of the eyepiece is 5.0 cm. If an object is 100 m away from the objective lens, where is the final image of the eyepiece? What is its magnification?
An object is 20 cm in front of a lens of focal length 9.5 cm. A second lens of focal length -30 cm is 15 cm behind the first lens. Find the location of the final image and its magnification.
A diverging lens with f = -20 cm is placed 12 cm to the left of a converging lens of f = 35 cm. If a 20 m tall object is 50 cm to the left of the diverging lens, where is the final image located and how tall is the image?
When Mars is nearest the Earth, the distance separating the two planets is 88.6 x 106 km. Mars is viewed through a telescope whose mirror has a diameter of 30.0 cm. If the wavelength of the light is 590 nm, what is the smallest distance that can be resolved between the two points on Mars?
