Lenz's Law Examples
A metal rod is moved to the right through a magnetic field. A charge separation is induced as shown below. Determine the direction of the magnetic field.
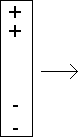
Lenz's law states that:
The current induced in a circuit due to a change in a magnetic field is directed to oppose the change in flux and to exert a mechanical force which opposes the motion.
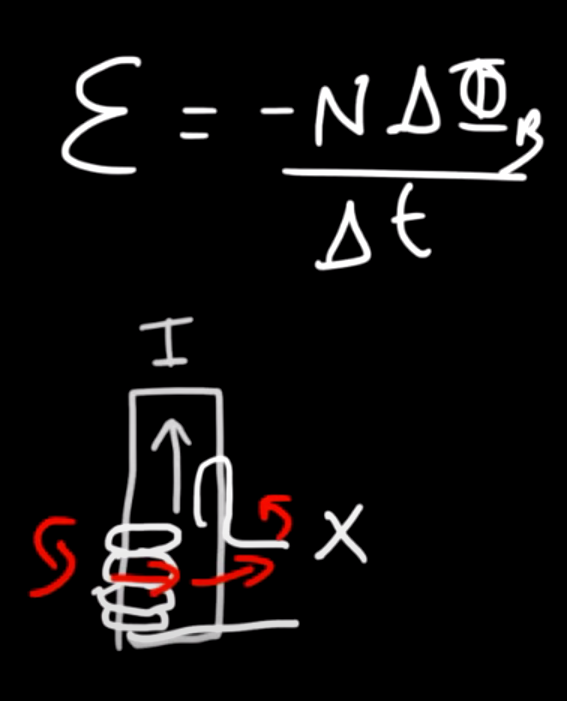
Lenz's law is a fundamental principle in electromagnetism that describes the direction of induced currents in response to changing magnetic fields. It states that an induced current will flow in a direction such that its magnetic field opposes the change in the magnetic flux that caused it. For instance, if a magnetic field through a coil increases, the induced current will generate a magnetic field opposing this increase. To solve problems involving Lenz's law, follow these steps: first, determine the direction of the change in the magnetic flux; next, identify the direction of the induced magnetic field that would oppose this change; and finally, use the right-hand rule to find the direction of the induced current. By applying Lenz's law, you can predict how systems will respond to changes in magnetic environments, providing valuable insights into the behavior of inductive components in circuits.
Related Problems
As a steel guitar string vibrates, the component of the magnetic field perpendicular to the area of a pickup coil nearby is given by B(t) = 50 mT + (3.20 mT) Sin (1046t). The circular pickup coil has 30 turns, a radius of 2.70 mm, and a resistance of 0.10 . What is the magnitude of the maximum current induced in the coil?
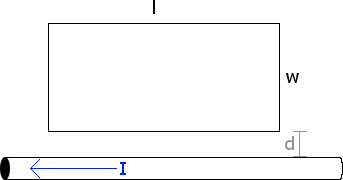
A square coil, with dimensions l = 12.0 cm, w = 7.0 cm, is placed d = 3.0 cm above a wire that carries a current of 30.0 A. Find the magnetic flux through the wire.
A current carrying loop has a radius of 3 cm. The current is 7 A in the counter clockwise direction. Find the magnetic dipole moment,
The wire depicted below has a current I = 25.0 A, r = 9.0 cm and r = 6.0 cm. Find the magnetic dipole moment .