Gauss's Law Sphere
Use Gauss's law to find the electric field around a conducting sphere of radius R, both within and outside the sphere. That is for a distance rR. (this is a calculus based derivation)
Related Problems
Two point charges, q = 6Q and q = -2Q, are separated by a distance, d. The attractive force between these two particles is 20 N. If the distanced is halved, so d = d/2, what is the new force between the particles?
Two metal spheres are charged, q = 6Q and q = -2Q, and are separated by a distance d. The attractive force between these two spheres is 20 N. The metal spheres are then brought together so they are touching, and then separated again a distance d. What is the new charge on the metal spheres and what is the new force between them?
Two objects, whose charges are +3 nC and -2 nC, are separated by 1.0 mm. Find the magnitude of the attractive force that either charge exerts on the other.
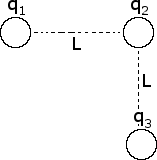
In the figure below, L = 1.0 mm, q = +3 nC, q = -2 nC, and q is +4 nC. Find the magnitude and direction of the net electrostatic force on q