Dynamic Physics
The large block m is 10 kg, and the smaller block m is 1 kg. The coefficient of kinetic friction is 0.1. Determine the acceleration of the system and the contact force between the blocks. The applied force, F is 30 N. Also draw a free body diagram for both blocks.
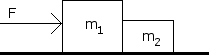 SOLUTION MISSING: Unfortunately the author of this youtube video removed their content. You may be able to find a similar problem by checking the other problems in this subject. If you want to contribute, leave a comment with the link to your solution.
SOLUTION MISSING: Unfortunately the author of this youtube video removed their content. You may be able to find a similar problem by checking the other problems in this subject. If you want to contribute, leave a comment with the link to your solution.Related Problems
An Object with mass m and initial velocity v is brought to rest by a constant force F acting for a time t and through a distance d. Possible expressions for the magnitude of the force F are: i. ii. iii.
ii only
iii only
i and ii only
ii and iii only
i, ii, and iii
A toy car of mass 6 kg moving in a straight path, experiences a net force given by the function F = -3t. At time t=0, the car has a velocity of 4 m/s in the positive direction and is located +8 m from the origin. The car will come instantaneously to rest at time t equal to
2/3 s
sqrt( 4/3 ) s
sqrt( 8/3 ) s
sqrt( 8) s
4 s
The large block m is 6 kg, and the smaller block m is 12 kg. The coefficient of kinetic friction is 0.2. Determine the acceleration of the system and the Tension T . The applied force, F is 36 N. Also draw a free body diagram for both blocks.
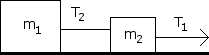
A ball of mass M is thrown vertically upward with an initial speed of v0. It experiences a force of air resistance given by F=−kv, where k is a positive constant. The positive direction for all vector quantities is upward. Express all algebraic answers in terms of M, k, v0, and fundamental constants.
Does the magnitude of the acceleration of the ball increase, decrease, or remain the same as the ball moves upward?
Write, but do NOT solve, a differential equation for the instantaneous speed vof the ball in terms of time tas the ball moves upward.
Determine the terminal speed of the ball as it moves downward.
Does it take longer for the ball to rise to its maximum height or to fall from its maximal height back to the height from which it was thrown? Justify your answer.
Sketch a graph of velocity versus time for the upward and downward parts of the ball’s flight, where is the time at which the ball returns to the height from which it was thrown.