Trig Function Derivatives
Find the derivative of the trig function,
Solving derivatives of trigonometric functions involves applying fundamental differentiation rules and understanding the specific derivatives of basic trigonometric functions. The key strategies include memorizing the standard derivatives listed on this page. For more complex functions, use the chain rule, product rule, or quotient rule as needed. The chain rule is particularly useful when differentiating composite functions, while the product and quotient rules handle functions that are multiplied or divided by each other.
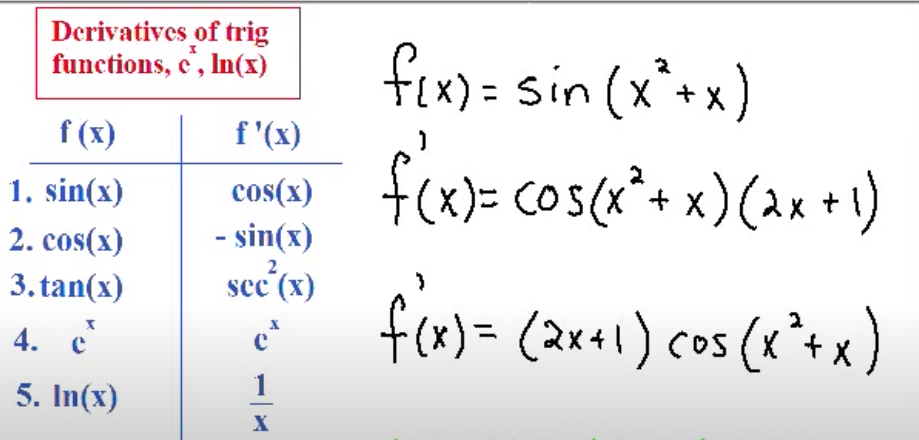
Posted by Adam Jensen 2 years ago
Related Problems
Show that the derivative of is equal to
Show that the derivative of is equal to
Use the quotient rule to find the derivative of
What is the derivative of